| Table of Subpages |
|---|
Overview
| Table of Contents |
|---|
Research
|
My research develops logics for dynamical systems to characterize the logical foundations of cyber-physical systems and to answer the question how we can |
|
Whether in cars, aircraft, or robots, the decisions that their computer programs reach have a crucial impact on all of us and they have the potential to make the world a better place. Computer programs can help us drive cars, help pilots fly aircraft, and enable robots to help the humans that they are interacting with. Along with these exciting prospects comes the responsibility to get the programs correct, though, which is quite a difficult challenge in light of the vagaries and uncertainties of the physical world.
My research group is pursuing this challenge with three related thrusts [IJCAR'16]:
- The design of mathematically grounded programming languages for dynamical systems that make it possible to unambiguously describe the behavior of a computer control program and its interaction with a physical model and to reason about its effect in logic.
- The design and realization of practical proof systems for those logics that make it possible to efficiently analyze the safety of a dynamical system.
- Making use of these capabilities by analyzing challenging applications in our prover KeYmaera X.
Logic and Programming Languages for Dynamical Systems
|
Logics of dynamical systems study logics and proof principles for properties of dynamical systems. Dynamical systems are mathematical models describing how the state of a system evolves over time. They are important in modeling and understanding many applications, including embedded systems and cyber-physical systems (CPSs). CPSs combine cyber capabilities (computation and/or communication) with physical capabilities (motion or other physical processes) to solve problems that no part could solve alone. Cars, aircraft and robots are prime examples, because they move physically in space in a way that is determined by discrete computerized control algorithms. Designing these algorithms to control CPSs is challenging due to their tight coupling with physical behavior. At the same time, it is vital that these algorithms be correct, since we rely on CPSs for safety-critical tasks like keeping aircraft from colliding. |
|
"How can we provide people with cyber-physical systems they can bet their lives on?" [Jeannette Wing]
In our group, we develop the Logical Foundations of Cyber-physical Systems and study the use of logics of dynamical systems and their programming languages in formal verification and validation of CPS. This relatively young area is a promising direction for future research, unique in its manifold connections to other pure and applied sciences, including many areas of mathematics, physics, and control theory. [details]
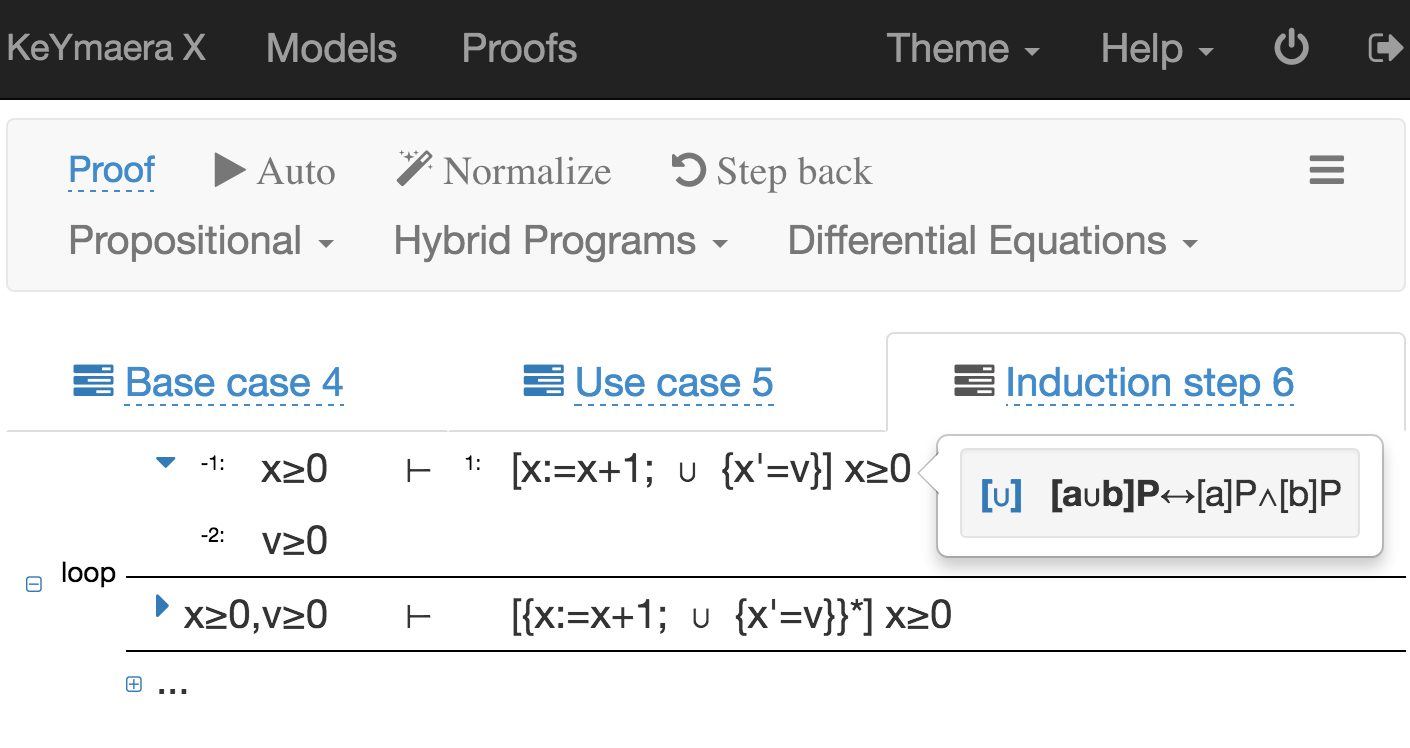
KeYmaera X: An aXiomatic Tactical Theorem Prover for Hybrid Systems
|
KeYmaera X is our theorem prover for logics for dynamical systems, especially hybrid systems with mixed discrete and continuous dynamics. Reasoning about complicated hybrid systems requires support for sophisticated proof techniques and efficient computation. KeYmaera X allows users to specify custom proof search techniques as tactics, execute tactics in parallel, and interface with partial proofs via an extensible user interface. |
|
KeYmaera X is built up from a small trusted core. The core contains a finite list of locally sound axioms (about 50) that are instantiated using a uniform substitution proof rule. Isolating all soundness-critical reasoning in this axiomatic core obviates the otherwise intractable task of ensuring that proof search algorithms are implemented correctly. This enables advanced proof search features---such as aggressive, speculative proof search and user-defined tactics built using a flexible proof tactic language---without correctness concerns that could undermine the usefulness of automated analysis. [details]
Applications
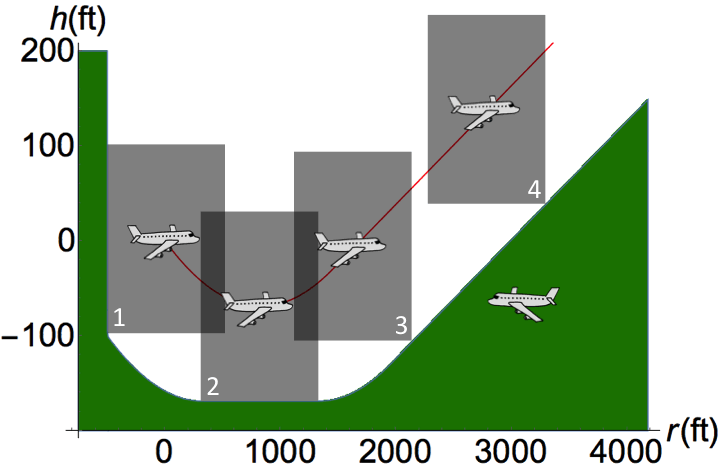
Logics of dynamical systems have already been instrumental in verifying many applications, including the Federal Administration Aviation (FAA)'s Next-Generation Airborne Collision Avoidance System ACAS X, the European Train Control System ETCS and the Federal Railroad Administration (FRA)'s train control, automotive systems, mobile ground robot navigation, and a surgical robotic system for skull-base surgery. [details]