Differential Game Logic for Hybrid Games

Differential Game Logic

Differential game logic (dGL) is a logic for specifying and verifying properties of hybrid games, i.e. games that combine discrete, continuous, and adversarial dynamics. Unlike hybrid systems, hybrid games allow choices in the system dynamics to be resolved adversarially by different players with different objectives. The logic dGL can be used to study the existence of winning strategies for such hybrid games, i.e. ways of resolving the player's choices in some way so that he wins by achieving his objective for all choices of the opponent. Hybrid games are determined, i.e. from each state, one player has a winning strategy, yet computing their winning regions may take transfinitely many steps. The logic dGL, nevertheless, has a sound and complete axiomatization relative to any expressive logic. Separating axioms are identified that distinguish hybrid games from hybrid systems. Finally, dGL is proved to be strictly more expressive than the corresponding logic of hybrid systems by characterizing the expressiveness of both.

Keywords: differential game logic, game logic, hybrid games, axiomatization, expressiveness [2]

Differential game logic for hybrid games has been implemented in the KeYmaera X theorem prover based on the uniform substitution calculus for differential game logic [4,6].

Differential Hybrid Games

The ACM TOCL 2017 article introduces differential hybrid games, which combine differential games with hybrid games. In both kinds of games, two players interact with continuous dynamics. The difference is that hybrid games also provide all the features of hybrid systems and discrete games, but only deterministic differential equations. Differential games, instead, provide differential equations with input by both players, but not the luxury of hybrid games, such as mode switches and discrete or alternating interaction. This article augments differential game logic with modalities for the combined dynamics of differential hybrid games. It shows how hybrid games subsume differential games and introduces differential game invariants and differential game variants for proving properties of differential games inductively.

Keywords: differential games, hybrid games, differential game game logic, differential game invariants, partial differential equations, viscosity solutions, real algebraic geometry [3]

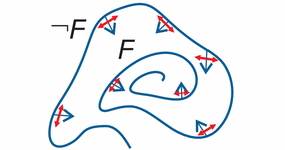
Differential Game Invariants

Differential game invariants [3] generalize differential invariance reasoning principles to differential games. Differential game invariants provide an inductive reasoning principle for differential games. A differential game is a differential equation x'=f(x,y,z) in which one player controls the choice of y while the opponent controls the choice of z. Even if the ultimate proof rule for differential game invariants is pleasantly simple, the major challenge was its soundness justification [3].

Constructive Differential Game Logic

Constructive differential game logic (CdGL) [8] is a constructive version of dGL enabling the constructive study of the existence of winning strategies in hybrid games with discrete, continuous, and adversarial dynamics. Constructive truth of CdGL formulas about hybrid games implies the constructive existence of winning strategies that are programs that win the hybrid game in question. This Curry-Howard correspondence ensures that constructive proofs for constructive hybrid games correspond to programs implementing their winning strategies.

Publications

1. Noah Abou El Wafa and André Platzer.
   Complete game logic with sabotage.
   In Pawel Sobocinski, Ugo Dal Lago and Javier Esparza, editors, Proceedings of the 39th Annual ACM/IEEE Symposium on Logic in Computer Science, LICS'24, pp. 1:1-1:15, ACM, 2024. © The authors
   [bib | ✂ | pdf | doi | slides | arXiv | abstract]
   
   
2. Brandon Bohrer and André Platzer.
   Refining constructive hybrid games.
   In Zena M. Ariola, editor, 5th International Conference on Formal Structures for Computation and Deduction, FSCD 2020, June 29 - July 5, Paris, France, Proceedings, volume 167 of LIPIcs, pp. 14:1-14:19. Schloss Dagstuhl - Leibniz-Zentrum für Informatik 2020. © The authors
   [bib | ✂ | pdf | doi | mypdf | slides | arXiv | abstract]
   
   
3. Brandon Bohrer and André Platzer.
   Constructive hybrid games.
   In Nicolas Peltier and Viorica Sofronie-Stokkermans, editors, Automated Reasoning, 10th International Joint Conference, IJCAR 2020, Paris, France, Proceedings, Part I, volume 12166 of LNCS, pp. 454-473. Springer 2020. © The authors
   [bib | ✂ | pdf | doi | mypdf | slides | arXiv | abstract]
   
   
4. Brandon Bohrer and André Platzer.
   Constructive game logic.
   In Peter Müller, editor, Programming Languages and Systems - 29th European Symposium on Programming, ESOP 2020, volume 12075 of LNCS, pp. 84-111. Springer, 2020. © The authors
   [bib | ✂ | pdf | doi | mypdf | slides | arXiv | abstract]
   
   
5. André Platzer.
   Uniform substitution at one fell swoop.
   In Pascal Fontaine, editor, International Conference on Automated Deduction, CADE-27, Natal, Brazil, Proceedings, volume 11716 of LNCS, pp. 425-441. Springer, 2019. © The author
   [bib | ✂ | pdf | doi | mypdf | slides | Isabelle | arXiv | errata | abstract]
   
   
6. André Platzer.
   Logical Foundations of Cyber-Physical Systems.
   Springer, Cham, 2018. 659 pages. ISBN 978-3-319-63587-3.
   [bib | ✂ | doi | slides | video | book | web | errata | abstract]
   
   
7. André Platzer.
   Uniform substitution for differential game logic.
   In Didier Galmiche, Stephan Schulz and Roberto Sebastiani, editors, Automated Reasoning, 9th International Joint Conference, IJCAR 2018, Oxford, UK, Proceedings, volume 10900 of LNCS, pp. 211-227. Springer 2018. © Springer
   [bib | ✂ | pdf | doi | slides | arXiv | abstract]
   
   
8. André Platzer.
   Differential hybrid games.
   ACM Trans. Comput. Log. 18(3), pp. 19:1-19:44, 2017. © The author
   [bib | ✂ | pdf | doi | mypdf | arXiv | abstract]
   
   
9. André Platzer.
   Differential game logic.
   ACM Trans. Comput. Log. 17(1), pp. 1:1-1:52, 2015. © The author
   [bib | ✂ | pdf | doi | mypdf | arXiv | errata | abstract]
   
   
10. André Platzer.
    Differential Game Logic for Hybrid Games.
    School of Computer Science, Carnegie Mellon University, CMU-CS-12-105, March 2012.
    Also see new results.
    [bib | ✂ | pdf | TOCL'15 | abstract]