|
⇓ Download ⇓
or get Source or read Book or watch Videos and follow Tutorial |
Overview
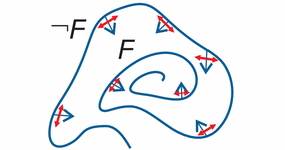
Differential invariants [1,4,5,13,21] provide induction principles for differential equations. They can be understood as the differential analogue of induction techniques but for differential equations rather than for discrete systems [11]. Discrete induction is used to prove a property of a loop by proving that the invariant is true initially and then that it is preserved every time the loop body executes once. Similarly, a differential invariant is proved to hold always after a differential equation by proving that it holds initially and by proving that it is preserved in the direction of the dynamics of the differential equation. Differential invariants can prove properties of differential equations without having to solve the equations, which makes them computationally attractive. Together with their cousins (differential cuts and differential ghosts), differential invariants give a complete axiomatization of analytic invariants [26].
Differential Invariants
Differential invariants [1,4] define an induction principle for differential equations [11,21]. They make it possible to prove properties of differential equations without having to solve the equations. Differential invariants are formulas that remain true along the dynamics of the hybrid system and its differential equations. The central property of differential invariants for verification purposes is that they replace infeasible or impossible reachability analysis with feasible symbolic computation. Differential invariants are computationally attractive concepts, because their inductive conditions are formed by differentials or Lie derivatives, giving decidable first-order real arithmetic.

Differential invariants have been studied in a number of results [1,13,14,11,18,20,7,21]. Together with the other invariant principles for differential equations explained below, they make differential equation invariants decidable [24].
Differential invariants (and their companions below) have been implemented in the KeYmaera theorem prover, its successor KeYmaera X, in Isabelle/HOL, and the Rocq proof assistant. [ [12,21,26] | Video ]
Differential Variants
The dual verification technique of differential variants can be used to prove liveness and progress properties of differential equations without having to solve them. Differential variants [1] are implemented in KeYmaera. More sophisticated proof techniques for liveness and progress properties of differential equations [27] are available in KeYmaera X.

More generally, every true open liveness property of compact initial value problems can be proved in differential dynamic logic [29].
Differential Cuts
Differential cuts [1,4,13,21] allow the use of lemmas that have been proved for differential equations. Differential cuts work as follows. They first prove that a differential equation never leaves region C and then restrict the dynamics of the system to C. Restricting the dynamics of a system to a subregion C usually changes the behavior of the system, except that the first proof already showed a lemma that the system cannot leave region C anyhow, so that the restriction of the dynamics to C turns out to be a pseudo-restriction that does not change the actual dynamics even if it changes the description.

The no differential cut elimination theorem [13] has been proved, which implies that differential cuts cannot be eliminated but fundamentally add to the deductive power. Sometimes you crucially need to exploit differential cuts to be able to verify. [ [12,21,26] | Video ]
Differential Ghosts
Ghost variables (or auxiliary variables) are extra variables that remember intermediate states, which can be useful for proving properties of conventional discrete programs. Differential ghosts [13,21] are the differential counterpart. What differential ghosts do is that they introduce extra variables into extra dimensions of the system, which can further evolve according to extra differential equations that are made up solely for the purposes of the proof. Differential ghosts are an integral part of the complete axiomatization of differential equations [24,26].

Differential Equation Axiomatization
By crucially exploiting differential ghosts, it has been shown that invariance properties of differential equations are decidable [24,26] just by conducting a corresponding proof/disproof from these axiomatic reasoning principles for differential equations.
This research proves the completeness of an axiomatization for differential equation invariants described by Noetherian functions. First, the differential equation axioms of differential dynamic logic are shown to be complete for reasoning about analytic invariants. Completeness crucially exploits differential ghosts, which introduce additional variables that can be chosen to evolve freely along new differential equations. Cleverly chosen differential ghosts are the proof-theoretical counterpart of dark matter. They create new hypothetical state, whose relationship to the original state variables satisfies invariants that did not exist before. The reflection of these new invariants in the original system then enables its analysis.
An extended axiomatization with existence and uniqueness axioms is complete for all local progress properties, and, with a real induction axiom, is complete for all semianalytic invariants. This parsimonious axiomatization serves as the logical foundation for reasoning about invariants of differential equations. Indeed, it is precisely this logical treatment that enables the generalization of completeness to the Noetherian case. [ [24,26] | Video ]
Furthermore, every true bounded open safety property of compact initial value problems can be proved in differential dynamic logic [29].
Differential Radical Invariants
A generalization of differential invariants to higher-order derivatives, called differential radical invariants, gives a decision procedure for algebraic invariants of algebraic differential equations. Differential radical invariants decide equational invariants p=0 for polynomials p. Differential radical invariants [16] are implemented in KeYmaera. More general complete axiomatic invariant proving [26] is available in KeYmaera X.
 |
Differential Game Invariants
Differential game invariants [22] generalize differential invariance reasoning principles to differential games. Differential game invariants function quite similar to differential invariants, except that they are not limited to differential equations but also work for differential games. A differential game is a differential equationx'=f(x,y,z) in which one player controls the choice of y while the opponent controls the choice of z.
Selected Publications
The canonical reference on differential invariants is the article in the Journal of Logic and Computation [1] that appeared in 2008. Differential invariants were later used for a fixpoint procedure that computes differential invariants and verifies some interesting hybrid systems automatically , which appeared at CAV'08 [3] and in a special issue of FMSD for selected CAV papers [5]. An elegant axiomatic formulation of differential invariants, differential cuts, and differential ghosts has been reported at CADE-25 [19] and JAR [21], which was subsequently exploited for a complete differential equation axiomatization at LICS'18 [24], including analytic and semianalytic invariants in J. ACM [26]. Also see publications on differential invariants and the publication reading guide.-
André Platzer and Long Qian.
Axiomatization of compact initial value problems: Open properties.
J. ACM 72(6), pp. 41:1-41:51, 2025. © The authors
[bib | ⧉ | pdf | doi | arXiv | abstract]
-
Yong Kiam Tan and André Platzer.
Deductive stability proofs for ordinary differential equations.
In Jan Friso Groote and Kim G. Larsen, editors, Tools and Algorithms for the Construction and Analysis of Systems, TACAS 2021, Proceedings, Part II, volume 12652 of LNCS, pp. 181–199. Springer, 2021. © The authors
[bib | ⧉ | pdf | doi | mypdf | slides | video | kyx | arXiv | abstract]
-
Yong Kiam Tan and André Platzer.
An axiomatic approach to existence and liveness for differential equations.
Formal Aspects of Computing 33(4), pp. 461-518, 2021.
Special issue for selected papers from FM'19. © The authors
[bib | ⧉ | pdf | doi | mypdf | arXiv | FM'19 | abstract]
-
André Platzer and Yong Kiam Tan.
Differential equation invariance axiomatization.
J. ACM 67(1), pp. 6:1-6:66, 2020. © The authors
[bib | ⧉ | pdf | doi | slides | video | arXiv | LICS'18 | abstract]
-
Yong Kiam Tan and André Platzer.
An axiomatic approach to liveness for differential equations.
In Maurice ter Beek, Annabelle McIver, and José N. Oliviera, editors, FM 2019: Formal Methods - The Next 30 Years, volume 11800 of LNCS, pp. 371-388. Springer, 2019. © Springer
[bib | ⧉ | pdf | doi | slides | arXiv | FAC'21 | abstract]
-
André Platzer and Yong Kiam Tan.
Differential equation axiomatization:
The impressive power of differential ghosts.
In Anuj Dawar and Erich Grädel, editors, Proceedings of the 33rd Annual ACM/IEEE Symposium on Logic in Computer Science, LICS'18, pp. 819-828. ACM 2018. © The authors
[bib | ⧉ | pdf | doi | slides | video | arXiv | JACM'20 | abstract]
-
André Platzer.
Logical Foundations of Cyber-Physical Systems.
Springer, Cham, 2018. 659 pages. ISBN 978-3-319-63587-3.
[bib | ⧉ | doi | slides | video | book | web | errata | abstract]
-
André Platzer.
Differential hybrid games.
ACM Trans. Comput. Log. 18(3), pp. 19:1-19:44, 2017. © The author
[bib | ⧉ | pdf | doi | arXiv | abstract]
-
André Platzer.
A complete uniform substitution calculus for differential dynamic logic.
Journal of Automated Reasoning 59(2), pp. 219-265, 2017. © The author
[bib | ⧉ | pdf | doi | mypdf | arXiv | abstract]
-
Andrew Sogokon, Khalil Ghorbal, Paul B. Jackson and André Platzer.
A method for invariant generation for polynomial continuous systems.
In Barbara Jobstmann and K. Rustan M. Leino, editors, Verification, Model Checking, and Abstract Interpretation - 17th International Conference, VMCAI 2016, St. Petersburg, Florida, USA, January 17-19, 2016, Proceedings, volume 9583 of LNCS, pp. 268-288. Springer, 2016. © Springer
[bib | ⧉ | pdf | doi | slides | abstract]
-
André Platzer.
A uniform substitution calculus for differential dynamic logic.
In Amy P. Felty and Aart Middeldorp, editors, International Conference on Automated Deduction, CADE-25, Berlin, Germany, Proceedings, volume 9195 of LNCS, pp. 467-481. Springer, 2015. © Springer
[bib | ⧉ | pdf | doi | slides | arXiv | JAR'17 | abstract]
-
Khalil Ghorbal, Andrew Sogokon, and André Platzer.
A hierarchy of proof rules for checking differential invariance of algebraic sets.
In Deepak D'Souza, Akash Lal, and Kim Guldstrand Larsen, editors, Verification, Model Checking, and Abstract Interpretation - 16th International Conference, VMCAI 2015, Mumbai, India, January 12-14, 2015, Proceedings, volume 8931 of LNCS, pp. 431-448. Springer, 2015. © Springer
[bib | ⧉ | pdf | doi | slides | study | ComLan'17 | abstract]
-
Khalil Ghorbal, Andrew Sogokon, and André Platzer.
Invariance of conjunctions of polynomial equalities for algebraic differential equations.
In Markus Müller-Olm and Helmut Seidl, editors, 21st International Static Analysis Symposium, SAS 2014, volume 8723 of LNCS, pp. 151-167. Springer, 2014. © Springer
[bib | ⧉ | pdf | doi | slides | study | abstract]
-
Khalil Ghorbal and André Platzer.
Characterizing algebraic invariants by differential radical invariants.
In Erika Ábrahám and Klaus Havelund, editors, Tools and Algorithms for the Construction and Analysis of Systems, TACAS 2014, Proceedings, volume 8413 of LNCS, pp. 279-294. Springer, 2014. © Springer
[bib | ⧉ | pdf | doi | slides | study | TR | abstract]
-
André Platzer.
Dynamic logics of dynamical systems.
arXiv:1205.4788, May 2012. Long version of LICS'12 invited tutorial.
[bib | ⧉ | pdf | arXiv | LICS'12 | abstract]
-
André Platzer.
A differential operator approach to equational differential invariants.
In Lennart Beringer and Amy Felty, editors, Interactive Theorem Proving, International Conference, ITP 2012, August 13-15, Princeton, USA, Proceedings, volume 7406 of LNCS, pp. 28-48. Springer, 2012. © Springer
Invited paper.
[bib | ⧉ | pdf | doi | slides | abstract]
-
André Platzer.
The structure of differential invariants and differential cut elimination.
Logical Methods in Computer Science 8(4), pp. 1-38, 2012. © The author
[bib | ⧉ | pdf | doi | mypdf | arXiv | abstract]
-
André Platzer.
Logics of dynamical systems.
ACM/IEEE Symposium on Logic in Computer Science, LICS 2012, June 25–28, 2012, Dubrovnik, Croatia, pp. 13-24. IEEE 2012. © IEEE
Invited paper.
[bib | ⧉ | pdf | doi | slides | abstract]
-
André Platzer.
The complete proof theory of hybrid systems.
ACM/IEEE Symposium on Logic in Computer Science, LICS 2012, June 25–28, 2012, Dubrovnik, Croatia, pp. 541-550. IEEE 2012. © IEEE
[bib | ⧉ | pdf | doi | slides | TR | abstract]
-
André Platzer.
The Complete Proof Theory of Hybrid Systems.
School of Computer Science, Carnegie Mellon University, CMU-CS-11-144, November 2011.
[bib | ⧉ | pdf | LICS'12]
-
André Platzer.
Logic and compositional verification of hybrid systems.
In Ganesh Gopalakrishnan and Shaz Qadeer, editors, Computer Aided Verification, CAV 2011, Snowbird, UT, USA, Proceedings, volume 6806 of LNCS, pp. 28-43. Springer, 2011. © Springer
Invited tutorial.
[bib | ⧉ | pdf | doi | slides | abstract]
-
André Platzer.
Quantified differential invariants.
In Emilio Frazzoli and Radu Grosu, editors, Proceedings of the 14th ACM International Conference on Hybrid Systems: Computation and Control, HSCC 2011, Chicago, USA, April 12-14, pp. 63-72. ACM, 2011. © ACM
[bib | ⧉ | pdf | doi | slides | abstract]
-
André Platzer.
Logical Analysis of Hybrid Systems:
Proving Theorems for Complex Dynamics.
Springer, Heidelberg, 2010. 426 pages. ISBN 978-3-642-14508-7.
[bib | ⧉ | doi | book | web | errata | abstract]
-
André Platzer and Edmund M. Clarke.
Formal verification of curved flight collision avoidance maneuvers: A case study.
In Ana Cavalcanti and Dennis Dams, editors, 16th International Symposium on Formal Methods, FM, Eindhoven, Netherlands, Proceedings, volume 5850 of LNCS, pp. 547-562. Springer, 2009. © Springer
FM Best Paper Award.
[bib | ⧉ | pdf | doi | slides | study | TR | abstract]
-
André Platzer and Edmund M. Clarke.
Computing differential invariants of hybrid systems as fixedpoints.
Formal Methods in System Design 35(1), pp. 98-120, 2009.
Special issue for selected papers from CAV'08. © Springer
[bib | ⧉ | pdf | doi | study | CAV'08 | abstract]
-
André Platzer.
Differential Dynamic Logics:
Automated Theorem Proving for Hybrid Systems.
PhD Thesis, Department of Computing Science, University of Oldenburg, 2008.
ACM Doctoral Dissertation Honorable Mention Award in 2009.
Extended version appeared as book Logical Analysis of Hybrid Systems: Proving Theorems for Complex Dynamics, Springer, 2010.
[bib | ⧉ | pdf | eprint | slides | book | ebook | abstract]
-
André Platzer and Edmund M. Clarke.
Computing differential invariants of hybrid systems as fixedpoints.
In Aarti Gupta and Sharad Malik, editors, Computer Aided Verification, CAV 2008, Princeton, USA, Proceedings, volume 5123 of LNCS, pp. 176-189, Springer, 2008. © Springer
[bib | ⧉ | pdf | doi | slides | study | TR | FMSD'09 | abstract]
-
André Platzer and Edmund M. Clarke.
Computing Differential Invariants of Hybrid Systems as Fixedpoints.
School of Computer Science, Carnegie Mellon University, CMU-CS-08-103, Feb, 2008.
[bib | ⧉ | pdf | CAV'08]
-
André Platzer.
Differential-algebraic dynamic logic for differential-algebraic programs.
Journal of Logic and Computation 20(1), pp. 309-352, 2010.
Special issue for selected papers from TABLEAUX'07. © The author
[bib | ⧉ | pdf | doi | eprint | study | errata | TABLEAUX'07 | abstract]
For full details, please see my List of Publications.
 |
Any opinions, findings, and conclusions or recommendations expressed are those of the author(s) and do not necessarily reflect the views of any sponsoring institution.
