|
Schedule | ||||||||||||||
|

|
- DESCRIPTION:
-
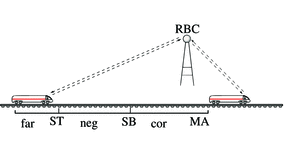
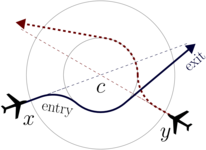
Hybrid systems are models for complex physical systems and have become a widely used concept for understanding their behaviour. Many applications are safety-critical, including car, railway, and air traffic control, robotics, physical-chemical process control, and biomedical devices. Hybrid systems analysis studies how we can build computerized controllers for physical systems which are guaranteed to meet their design goals.
 |
 |
 |
 |
 |
 |
-
This course covers mathematical models for complex physical systems, including discrete dynamical systems, continuous dynamical systems, real-time dynamical systems, and hybrid dynamical systems (or hybrid systems for short). Our primary focus will be on the mathematical foundations and analytic techniques for these complex systems. We will study the questions that are important for designing system models and for understanding their behaviour. We will emphasize concise representations of analytic problems in logic and their algorithmic solutions in automated theorem provers and model checkers.
The class will provide you with modern techniques for analyzing the correct functioning of important safety-critical systems ranging from embedded systems in cars and biomedical devices, over chemical/physical process control and chip design, to full car, aircraft, and train control. The opportunity to gain practical experience in analysis of cyber-physical systems will be given as part of the course. The class should be appropriate for graduate students and for advanced undergraduates with an interest in mathematical, logical, or formal analysis methods.
- OBJECTIVES:
- You will develop an understanding for important safety-critical aspects of embedded and cyber-physical systems. You will be able to understand and develop discrete/continuous/hybrid dynamical system models. You will learn how you can analyze if a hybrid system works as intended and if it actually meets its design goals. You will learn how to use formal methods and calculi to analyze system correctness and you will understand how automatic verification techniques work.
- PREREQUISITES:
- Basic knowledge in logic (e.g., propositional logic) and continuous mathematics (e.g., differential equations) is of advantage but not strictly required.
- TEXTBOOK:
-
-
André Platzer.
Logical Analysis of Hybrid Systems:
Proving Theorems for Complex Dynamics.
Springer, Heidelberg, 2010. 426 pages. ISBN 978-3-642-14508-7.
[bib | ✂ | doi | book | web | errata | abstract]

-
André Platzer.
- METHOD OF EVALUATION:
-
Grading will be based on a set of homework assignments, including hands-on analysis experience, midterm exam, and a final project (30% Homework, 15% Midterm, 55% Project).
The project is worth 260 points, with 20 points for the whitepaper, 50 points for the proposal, and 190 points for the project report. - MORE INFORMATION:
- See case studies for some illustrations and examples of hybrid system applications.
- TOPICS TO BE COVERED:
-
- Safety-critical complex physical systems
- Discrete dynamical systems
- Continuous dynamical systems
- Hybrid dynamical systems
- Differential equations (select topics like Peano, Picard-Lindelöff)
- Controllability, safety & stability
- First-order logic
- First-order real arithmetic
- Real-closed fields and semialgebraic geometry
- Numerical analysis and integration
- Symbolic reachability analysis
- Computable analysis
- Hybrid programs and hybrid automata
- Compositionality
- Dynamic logic & dynamical systems
- Differential dynamic logic
- Disturbances in hybrid control
- Deduction modulo
- Differential variance and invariance
- Differential closure properties
- Differential-algebraic equations and differential algebra
- Differential transformations and differential reductions
- Railway control applications
- Air traffic control applications
- Distributed car control applications
- Time permitting: Nullstellensätze and Positivstellensätze
- Time permitting: Gröbner bases and algebraic geometry
- Time permitting: Proof theory of hybrid systems
- Time permitting: Fixedpoint model checking engines
