KeYmaera: A Hybrid Theorem Prover for Hybrid Systems

Table of Contents
  1. Overview
  2. Case Studies
  3. KeYmaera Tool Architecture
  4. News
  5. Verification
  6. Download, Documentation & Tutorials
  7. Statistics
  8. Etymology: The Name KeYmaera
  9. Abstract
  10. Selected Publications
Download or
Launch
KeYmaera
Logical Analysis of Hybrid Systems

Overview
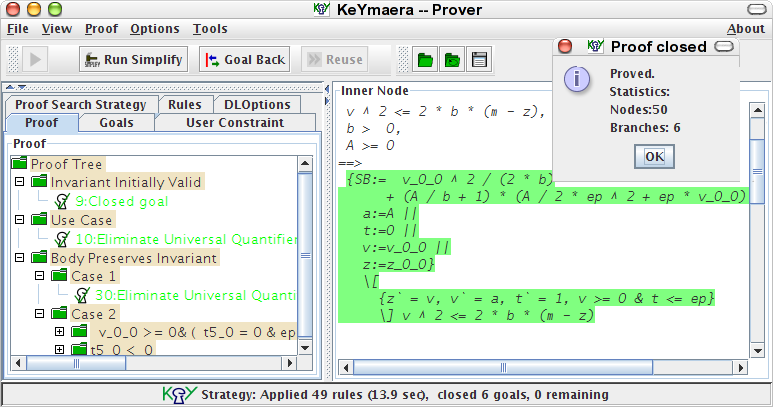
KeYmaera is a hybrid verification tool for hybrid systems that combines deductive, real algebraic, and computer algebraic prover technologies. It is an automated and interactive theorem prover for a natural specification and verification logic for hybrid systems. KeYmaera supports differential dynamic logic (dL) [36,34,13], which is a first-order dynamic logic for hybrid programs [36,34,13], a program notation for hybrid systems. KeYmaera also supports hybrid systems with nonlinear discrete jumps, nonlinear differential equations, differential-algebraic equations, differential inequalities, and systems with nondeterministic discrete or continuous input. For automation, KeYmaera implements a free-variable sequent calculus and automatic proof strategies that decompose the hybrid system specification symbolically. This compositional verification principle helps scaling up verification, because KeYmaera verifies a big system by verifying properties of subsystems. To overcome the complexity of real arithmetic, we integrate real quantifier elimination following an iterative background closure strategy [35,26]. The KeYmaera verification tool is particularly suitable for verifying parametric hybrid systems and has been used successfully for verifying case studies from train control [23,21], car control [18,16], and air traffic control [24,21].

The KeYmaera verification tool provides significant automation (up to 100%). It handles differential equations and integrates full first-order real arithmetic. KeYmaera also implements differential invariants [33]. KeYmaera implements procedures for automatically generating invariants and differential invariants [30,27,7], but allows you to specify invariants interactively whenever your case study is too complex for KeYmaera's current automation. The graphical user interface of KeYmaera can be used to navigate and manipulate the proofs discovered by KeYmaera or find more efficient proofs.

Details about the KeYmaera verification approach can be found in the corresponding book [21] and several other publications.

Case Studies

The KeYmaera verification tool has been used successfully for verification in railway [23], automotive [18,16,11], and aviation transportation systems [24,4], as well as autonomous robotics [1,6], surgical robotics [3], and electric circuits [21].

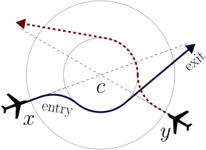
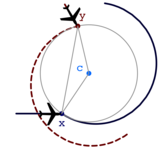
KeYmaera has been used for automatic verification of collision freedom for the cooperation layer of the European Train Control System (ETCS) [23]. It has been used systematically to synthesize the required safety constraints on the design parameters of fully parametric ETCS [23]. KeYmaera has been used to verify collision freedom in roundabout aircraft collision avoidance maneuvers [33], including the flyable roundabout collision avoidance maneuver [24]. These verification results show that the controllers of the aircraft models successfully prevent collisions. Extensions for provable collision freedom in flyable disc maneuvers for an arbitrary number of aircraft have been verified in KeYmaeraD [4]. A whole range of automotive systems have been verified with KeYmaera, including collision freedom in adaptive cruise control for highway systems [18], safety of a CICAS-inspired intersection control system for cars [16], safe interactions of cars with traffic centers via variable speed limits, including moving incidents [11], and a model for CICAS-SLTA Signalized Left Turn Assist [8]. The dynamic window approach for autonomous robotic ground vehicles has been verified in KeYmaera [1]. A few academic standard examples from the hybrid systems world have been verified with KeYmaera as well, including a fully parametric version of the bouncing ball [28] and the standard, non-parametric water tank. KeYmaera has been used to verify the RLC electric circuit [21], a model of a distributed elevator controller, medical surgical robotics applications for skull base surgery [3], and a robotic factory automation case study [6].

 
 
 
 
 
 
 
 
 
 

For more details on case studies, also see the subpages on this web page and the projects listed in KeYmaera's project wizard (the menu item File->Load Project in KeYmaera).

Tell us if you want to advertise your case study or KeYmaera verification example on this web page and in the KeYmaera project wizard.

KeYmaera Tool Architecture

The architecture of the KeYmaera verification tool has a plug-in system for solvers and proof rules [28] and allows to adjust the automatic proof strategies by several options.

News

KeYmaera is actively developed and maintained. Its set of features and the download version are updated continuously. Recently released additions to KeYmaera include:

Verification

In KeYmaera, verifying correct functioning of hybrid systems amounts to proving corresponding formulas in, what is called, differential dynamic logic dL [36,34]. These formulas state the desired correctness properties of the hybrid systems under consideration, including safety, liveness, reactivity, and controllability properties. For showing that these systems operate as expected, André Platzer has devised a logical verification calculus [36,34].

Advanced verification technology for differential dynamic logics is further based on differential invariants [33,30,27], which are formulas that remain true along the dynamics of the hybrid system and its differential equations. Differential invariants and differential induction are essentially a generalization of discrete induction to differential equations. This verification technology for differential dynamic logic and differential-algebraic dynamic logic has been implemented in the KeYmaera theorem prover for hybrid systems.

KeYmaera implements the verification calculi for the logics described in [36,34,37,33,6] and also part of [20,9]. The verification algorithms implemented in KeYmaera are described in the papers [35,26,27,7] and, a little bit also in the KeYmaera tool paper [28].

Download, Documentation & Tutorials

LICS tutorial or
LICS slides or
Cheat Sheet or
User Guide or
Howto Guide

Statistics

KeYmaera is based on the KeY system and on computer algebra tools like Mathematica, Reduce, and the Orbital library. Including the graphical user interface and the KeY base system, the KeYmaera verification tool has

Note that, in theory, KeYmaera would only need a dozen axioms and proof rules [13]. KeYmaera nevertheless provides many more in order to make the reasoning more efficient and provide you with ways to handle common special cases easily.

Etymology: The Name KeYmaera

The name KeYmaera is a homophone to Chimaera (Χíμαιρα), the hybrid animal from ancient Greek mythology, which is a hybrid mixture of multiple animals. KeYmaera is a hybrid version of the KeY tool. KeYmaera also is a hybrid mixture of multiple proving technologies from logic or discrete and continuous mathematics and KeYmaera is intended for hybrid systems verification, which are systems evolving along mixed discrete and continuous transitions.

The development code name for KeYmaera was HyKeY, because HyKeY stands to reason as a canonical name in line with hybrid systems model checkers like HyTech or HySAT. We decided to go for a fancy name instead, paying homage to KeYmaera's roots in a hybrid extension of KeY, to its purpose for hybrid systems verification, and to the hybrid nature of its algorithmic design combining aspects of theorem proving, computer algebra, decision procedures, and model checking.

Abstract

KeYmaera is a hybrid verification tool for hybrid systems that combines deductive, real algebraic, and computer algebraic prover technologies. It is an automated and interactive theorem prover for a natural specification and verification logic for hybrid systems. KeYmaera supports differential dynamic logic [36,34], which is a real-valued first-order dynamic logic for hybrid programs, a program notation for hybrid automata. For automating the verification process, KeYmaera implements a generalized free-variable sequent calculus and automatic proof strategies that decompose the hybrid system specification symbolically. To overcome the complexity of real arithmetic, we integrate real quantifier elimination following an iterative background closure strategy. Our tool is particularly suitable for verifying parametric hybrid systems and has been used successfully for verifying collision avoidance in case studies from train control and air traffic management.

Keywords: dynamic logic, sequent calculus, automated theorem proving, decision procedures, computer algebra, verification of parametric hybrid systems, quantifier elimination

Selected Publications

The canonical references on the KeYmaera approach are [34,33,13]. The proof theory is studied in detail in [13]. The most comprehensive description of the KeYmaera appraoch can be found in the book [21], with further details also in subsequent papers. Also see publications on hybrid systems logic and the publication reading guide.
  1. Stefan Mitsch, Khalil Ghorbal, and André Platzer.
    On provably safe obstacle avoidance for autonomous robotic ground vehicles.
    Robotics: Science and Systems, 2013.
    [bib | pdf | study | abstract]

  2. André Platzer.
    A Complete Axiomatization of Differential Game Logic for Hybrid Games.
    School of Computer Science, Carnegie Mellon University, CMU-CS-13-100, January 2013.
    [bib | pdf | slides | abstract]

  3. Yanni Kouskoulas, David W. Renshaw, André Platzer and Peter Kazanzides.
    Certifying the safe design of a virtual fixture control algorithm for a surgical robot.
    In Calin Belta and Franjo Ivancic, editors, Hybrid Systems: Computation and Control (part of CPS Week 2013), HSCC'13, Philadelphia, PA, USA, April 8-13, 2013, pages 263-272. ACM, 2013. © ACM
    [bib | pdf | doi | study | abstract]

  4. Sarah M. Loos, David W. Renshaw, and André Platzer.
    Formal verification of distributed aircraft controllers.
    In Calin Belta and Franjo Ivancic, editors, Hybrid Systems: Computation and Control (part of CPS Week 2013), HSCC'13, Philadelphia, PA, USA, April 8-13, 2013, pages 125-130. ACM, 2013. © ACM
    [bib | pdf | doi | slides | poster | study | TR | abstract]

  5. André Platzer.
    Dynamic logics of dynamical systems.
    May 2012.
    [bib | pdf | arXiv | abstract]

  6. Jan-David Quesel and André Platzer.
    Playing hybrid games with KeYmaera.
    In Bernhard Gramlich, Dale Miller, and Ulrike Sattler, editors, Automated Reasoning, 6th International Joint Conference, IJCAR'12, Manchester, UK, Proceedings, volume 7364 of LNCS, pages 439-453. Springer, 2012. © Springer-Verlag
    [bib | pdf | doi | study | abstract]

  7. André Platzer.
    A differential operator approach to equational differential invariants.
    In Lennart Beringer and Amy Felty, editors, Interactive Theorem Proving, International Conference, ITP 2012, August 13-15, Princeton, USA, Proceedings, volume 7406 of LNCS, pages 28-48. Springer, 2012. © Springer-Verlag
    Invited paper.
    [bib | pdf | doi | slides | abstract]

  8. Nikos Aréchiga, Sarah M. Loos, André Platzer, and Bruce H. Krogh.
    Using theorem provers to guarantee closed-loop system properties.
    In Dawn Tilbury, editor, American Control Conference, ACC, Montréal, Canada, June 27-29. pages 3573-3580. 2012. © IEEE
    [bib | pdf | abstract]

  9. André Platzer.
    A complete axiomatization of quantified differential dynamic logic for distributed hybrid systems.
    Logical Methods in Computer Science, 8(4), pages 1-44, 2012.
    Special issue for selected papers from CSL'10.
    [bib | pdf | doi | arXiv | abstract]

  10. André Platzer.
    The structure of differential invariants and differential cut elimination.
    Logical Methods in Computer Science, 8(4), pages 1-38, 2012.
    [bib | pdf | doi | arXiv | abstract]

  11. Stefan Mitsch, Sarah M. Loos, and André Platzer.
    Towards formal verification of freeway traffic control.
    In Chenyang Lu, editor, ACM/IEEE Third International Conference on Cyber-Physical Systems, Beijing, China, April 17-19. pages 171-180, IEEE. 2012. © IEEE
    [bib | pdf | doi | slides | study | abstract]

  12. André Platzer.
    Logics of dynamical systems.
    ACM/IEEE Symposium on Logic in Computer Science, LICS 2012, June 25–28, 2012, Dubrovnik, Croatia, pages 13-24. IEEE 2012. © IEEE
    Invited paper.
    [bib | pdf | doi | slides | abstract]

  13. André Platzer.
    The complete proof theory of hybrid systems.
    ACM/IEEE Symposium on Logic in Computer Science, LICS 2012, June 25–28, 2012, Dubrovnik, Croatia, pages 541-550. IEEE 2012. © IEEE
    [bib | pdf | doi | slides | TR | abstract]

  14. André Platzer.
    Differential Game Logic for Hybrid Games.
    School of Computer Science, Carnegie Mellon University, CMU-CS-12-105, March 2012.
    Also see new results.
    [bib | pdf | abstract]

  15. André Platzer.
    The Complete Proof Theory of Hybrid Systems.
    School of Computer Science, Carnegie Mellon University, CMU-CS-11-144, November 2011.
    [bib | pdf | LICS'12 | abstract]

  16. Sarah M. Loos and André Platzer.
    Safe intersections: At the crossing of hybrid systems and verification.
    In Kyongsu Yi, editor, 14th International IEEE Conference on Intelligent Transportation Systems, ITSC'11, Washington, DC, USA, Proceedings, pages 1181-1186. 2011. © IEEE
    [bib | pdf | doi | slides | study | abstract]

  17. André Platzer.
    Logic and compositional verification of hybrid systems.
    In Ganesh Gopalakrishnan and Shaz Qadeer, editors, Computer Aided Verification, CAV 2011, Snowbird, UT, USA, Proceedings, volume 6806 of LNCS, pages 28-43. Springer, 2011. © Springer-Verlag
    Invited tutorial.
    [bib | pdf | doi | slides | abstract]

  18. Sarah M. Loos, André Platzer, and Ligia Nistor.
    Adaptive cruise control: Hybrid, distributed, and now formally verified.
    In Michael Butler and Wolfram Schulte, editors, 17th International Symposium on Formal Methods, FM, Limerick, Ireland, Proceedings, volume 6664 of LNCS, pages 42-56. Springer, 2011. © Springer-Verlag
    [bib | pdf | doi | slides | study | TR | abstract]

  19. André Platzer.
    Quantified differential invariants.
    In Emilio Frazzoli and Radu Grosu, editors, Proceedings of the 14th ACM International Conference on Hybrid Systems: Computation and Control, HSCC 2011, Chicago, USA, April 12-14, Pages 63-72. ACM, 2011. © ACM
    [bib | pdf | doi | slides | abstract]

  20. André Platzer.
    Quantified differential dynamic logic for distributed hybrid systems.
    In Anuj Dawar and Helmut Veith, editors, Computer Science Logic, 19th EACSL Annual Conference, CSL 2010, Brno, Czech Republic, August 23-27, 2010. Proceedings, volume 6247 of LNCS, pages 469-483. Springer, 2010. © Springer-Verlag
    [bib | pdf | doi | slides | TR | abstract]

  21. André Platzer.
    Logical Analysis of Hybrid Systems: Proving Theorems for Complex Dynamics.
    Springer, 2010. ISBN 978-3-642-14508-7.
    [bib | book | eBook | doi | web]

  22. André Platzer.
    Differential dynamic logic: Automated theorem proving for hybrid systems.
    Künstliche Intelligenz, 24(1), pages 75-77, 2010. © Springer-Verlag
    Invited paper.
    [bib | doi | abstract]

  23. André Platzer and Jan-David Quesel.
    European Train Control System: A case study in formal verification.
    In Karin Breitman and Ana Cavalcanti, editors, 11th International Conference on Formal Engineering Methods, ICFEM, Rio de Janeiro, Brasil, Proceedings, volume 5885 of LNCS, pages 246-265. Springer, 2009. © Springer-Verlag
    [bib | pdf | doi | slides | study | TR | abstract]

  24. André Platzer and Edmund M. Clarke.
    Formal verification of curved flight collision avoidance maneuvers: A case study.
    In Ana Cavalcanti and Dennis Dams, editors, 16th International Symposium on Formal Methods, FM, Eindhoven, Netherlands, Proceedings, volume 5850 of LNCS, pages 547-562. Springer, 2009. © Springer-Verlag
    This paper was awarded the FM Best Paper Award.
    [bib | pdf | doi | slides | study | TR | abstract]

  25. André Platzer.
    Verification of cyberphysical transportation systems.
    IEEE Intelligent Systems, 24(4), pages 10-13, Jul/Aug, 2009. © IEEE.
    Invited paper.
    [bib | doi | abstract]

  26. André Platzer, Jan-David Quesel, and Philipp Rümmer.
    Real world verification.
    In Renate A. Schmidt, editor, International Conference on Automated Deduction, CADE'09, Montreal, Canada, Proceedings, volume 5663 of LNCS, pages 485-501. Springer, 2009. © Springer-Verlag
    [bib | pdf | doi | slides | TR | smtlib | abstract]
    Introduces a decision procedure for universal nonlinear real arithmetic combining Gröbner bases and semidefinite programming for the Real Nullstellensatz. An extended set of real arithmetic benchmarks from KeYmaera is available in smtlib, including the examples from CADE'09 paper and from some other KeYmaera-related papers.

  27. André Platzer and Edmund M. Clarke.
    Computing differential invariants of hybrid systems as fixedpoints.
    Formal Methods in System Design, 35(1), pages 98-120, 2009. © Springer-Verlag
    Special issue for selected papers from CAV'08.
    [bib | pdf | doi | study | abstract]

  28. André Platzer and Jan-David Quesel.
    KeYmaera: A hybrid theorem prover for hybrid systems.
    In Alessandro Armando, Peter Baumgartner, and Gilles Dowek, editors, Automated Reasoning, Fourth International Joint Conference, IJCAR 2008, Sydney, Australia, Proceedings, volume 5195 of LNCS, pages 171-178. Springer, 2008. © Springer-Verlag
    [bib | pdf | doi | slides | tool | abstract]

  29. André Platzer.
    Differential Dynamic Logics: Automated Theorem Proving for Hybrid Systems.
    PhD Thesis, Department of Computing Science, University of Oldenburg, 2008.
    ACM Doctoral Dissertation Honorable Mention Award in 2009.
    Extended version appeared as book Logical Analysis of Hybrid Systems: Proving Theorems for Complex Dynamics, Springer, 2010.
    [bib | pdf | eprint | book | doi | web | abstract | slides]

  30. André Platzer and Edmund M. Clarke.
    Computing differential invariants of hybrid systems as fixedpoints.
    In Aarti Gupta and Sharad Malik, editors, Computer Aided Verification, CAV 2008, Princeton, USA, Proceedings, volume 5123 of LNCS, pages 176-189, Springer, 2008. © Springer-Verlag
    [bib | pdf | doi | slides | study | TR | abstract]

  31. André Platzer and Edmund M. Clarke.
    Computing Differential Invariants of Hybrid Systems as Fixedpoints.
    School of Computer Science, Carnegie Mellon University, CMU-CS-08-103, Feb, 2008.
    [bib | pdf | CAV'08 | abstract]

  32. André Platzer and Jan-David Quesel.
    Logical verification and systematic parametric analysis in train control.
    In Magnus Egerstedt and Bud Mishra, editors, Hybrid Systems: Computation and Control, 11th International Conference, HSCC 2008, St. Louis, USA, Proceedings, volume 4981 of LNCS, pages 646-649. Springer, 2008. © Springer-Verlag
    [bib | pdf | doi | abstract]

  33. André Platzer.
    Differential-algebraic dynamic logic for differential-algebraic programs.
    Journal of Logic and Computation, 20(1), pages 309-352, 2010. Advance Access published on November 18, 2008 by Oxford University Press.
    [bib | pdf | doi | study | abstract]

  34. André Platzer.
    Differential dynamic logic for hybrid systems.
    Journal of Automated Reasoning, 41(2), pages 143-189, 2008. © Springer-Verlag
    [bib | pdf | doi | study | abstract]

  35. André Platzer.
    Combining deduction and algebraic constraints for hybrid system analysis.
    In Bernhard Beckert, editor, 4th International Verification Workshop, VERIFY'07, Workshop at Conference on Automated Deduction (CADE), Bremen, Germany, CEUR Workshop Proceedings, 259:164-178, 2007.
    [bib | pdf | slides | abstract]

  36. André Platzer.
    Differential dynamic logic for verifying parametric hybrid systems.
    In Nicola Olivetti, editor, Automated Reasoning with Analytic Tableaux and Related Methods, International Conference, TABLEAUX 2007, Aix en Provence, France, July 3-6, 2007, Proceedings, volume 4548 of LNCS, pages 216-232. Springer, 2007. © Springer-Verlag
    This paper was awarded the TABLEAUX Best Paper Award.
    [bib | pdf | doi | slides | study | TR | abstract]

  37. André Platzer.
    A temporal dynamic logic for verifying hybrid system invariants.
    In Sergei Artemov and Anil Nerode, editors, Logical Foundations of Computer Science, International Symposium, LFCS 2007, New York, USA, Proceedings, volume 4514 of LNCS, pages 457-471. Springer, 2007. © Springer-Verlag
    [bib | pdf | doi | slides | study | TR | abstract]

  38. André Platzer.
    Differential logic for reasoning about hybrid systems.
    In Alberto Bemporad, Antonio Bicchi, and Giorgio Buttazzo, editors, Hybrid Systems: Computation and Control, 10th International Conference, HSCC 2007, Pisa, Italy, Proceedings, volume 4416 of LNCS, pages 746-749. Springer, 2007. © Springer-Verlag
    [bib | pdf | doi | abstract]

  39. André Platzer.
    Towards a hybrid dynamic logic for hybrid dynamic systems.
    In Patrick Blackburn, Thomas Bolander, Torben Braüner, Valeria de Paiva, and Jørgen Villadsen, editors, Proc., International Workshop on Hybrid Logic, HyLo 2006, Seattle, USA, Electr. Notes Theor. Comput. Sci. 174(6):63-77, 2007.
    [bib | pdf | doi | slides | abstract]

More details on the differential dynamic logic (dL), on the hybrid program model for hybrid systems, and on the principles of logic for hybrid systems. For full details, please see more publications.

Copyright © André Platzer        Last modified: 2013-05-02

Home | Publications | Research | Tools | Courses | A. Platzer