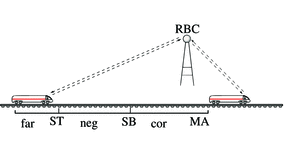
European Train Control System (ETCS)As one interesting case study for hybrid systems, we have successfully verified the cooperation layer of the fully parametric European Train Control System (ETCS) automatically in KeYmaera. We have also used our approach to discover the required safety constraints on the free parameters of ETCS for parametric verification. |
KeYmaera
or Source |
 |
 |
One simple example of one of the properties we have proved about ETCS is the following formula of differential dynamic logic. It expresses that for the state of a train controller train, the property z≤m always holds true when starting in a state where v2≤2b(m-z) is true:
Abstract
Complex physical systems have several degrees of freedom. They only work correctly when their control parameters obey corresponding constraints. Based on the informal specification of the European Train Control System (ETCS), we design a controller for its cooperation protocol. For its free parameters, we successively identify constraints that are required to ensure collision freedom. We formally prove the parameter constraints to be sharp by characterizing them equivalently in terms of reachability properties of the hybrid system dynamics. Using our deductive verification tool KeYmaera, we formally verify controllability, safety, liveness, and reactivity properties of the ETCS protocol that entail collision freedom. We prove that the ETCS protocol remains correct even in the presence of perturbation by disturbances in the dynamics. We verify that safety is preserved when a PI controlled speed supervision is used.
Keywords: formal verification of hybrid systems, train control, theorem proving, parameter constraint identification, disturbances [8]
Train Control with Air Pressure Brakes
Train control technology enhances the safety and efficiency of railroad operation by safeguarding the motion of trains to prevent them from leaving designated areas of operation and colliding with other trains. It is crucial for safety that the trains engage their brakes early enough in order to make sure they never leave the safe part of the track. Efficiency considerations, however, also require that the train does not brake too soon, which would limit operational suitability. It is surprisingly subtle to reach the right tradeoffs and identify the right control conditions that guarantee safe motion without being overly conservative.
In pursuit of an answer, we develop a hybrid system model with discrete control decisions for acceleration, brakes, and with continuous differential equations for their physical effects on the motion of the train. The resulting hybrid system model is systematically derived from the Federal Railway Administration model for flat terrain by conservatively neglecting minor forces.
The main contribution of this paper is the identification of a controller with control constraints that we formally verify to always guarantee collision freedom in the FRA model. The safe braking behavior of a train is influenced not only by the train configuration (e.g., train length and mass), but also by physical characteristics (e.g., brake pressure propagation and reaction time). We formalize train control safety properties in differential dynamic logic and prove the correctness of the train control models in the theorem prover KeYmaera X.
Keywords: Train control safety, Braking model verification, Performance analysis, Hybrid systems, Differential dynamic logic [9]
Train Control for Federal Railroad Administration Kinematics
Automated train control improves railroad operation by safeguarding the motion of trains while increasing efficiency by enabling motion within a safe envelope. Train controllers decide when to slow trains down to avoid collisions with other trains on the track, stay inside movement authorities, and navigate slopes, curves and tunnels safely. These systems must base their decisions on detailed motion models to guarantee the absence of overshoot of the movement authority (safety) and limit undershoot (efficiency). This paper is the first to formally verify the safety of the Federal Railroad Administration freight train kinematics model with all its relevant forces and parameters, including track slope and curvature, air brake propagation, and resistive forces as computed by the Davis equation. Due to the significant competing influence of these parameters on train stopping distances, even designing train controllers is a nontrivial control challenge, which we solve using formal verification. For increased generality at reduced verification effort, we verify symbolic mathematical generalizations of the train control models and subsequently apply efficient uniform substitutions to obtain verification results for physical train control models.
Keywords: Train control, Formal verification, Hybrid systems, Differential dynamic logic [10]
Selected Publications
Also see publications on verification of railway systems.
-
Aditi Kabra, Stefan Mitsch and André Platzer.
Verified train controllers for the Federal Railroad Administration train kinematics model: Balancing competing brake and track forces.
IEEE Trans. Comput. Aided Des. Integr. Circuits Syst. 41(11), pp. 4409-4420, 2022. Special issue for EMSOFT 2022. © IEEE
Best paper finalist
[bib | ⧉ | pdf | doi | slides | video | kyx | extra | abstract]
-
Stefan Mitsch, Marco Gario, Christof J. Budnik, Michael Golm and André Platzer.
Formal verification of train control with air pressure brakes.
In Alessandro Fantechi, Thierry Lecomte and Alexander Romanovsky, editors, RSSRail 2017: Reliability, Safety, and Security of Railway Systems, volume 10598 of LNCS, pp. 173-191. Springer, 2017. © Springer
[bib | ⧉ | pdf | doi | slides | abstract]
-
André Platzer and Jan-David Quesel.
European Train Control System: A case study in formal verification.
In Karin Breitman and Ana Cavalcanti, editors, 11th International Conference on Formal Engineering Methods, ICFEM'09, Rio de Janeiro, Brasil, Proceedings, volume 5885 of LNCS, pp. 246-265. Springer, 2009. © Springer
[bib | ⧉ | pdf | doi | slides | kyx | TR | old | abstract]
-
André Platzer.
Logical Analysis of Hybrid Systems:
Proving Theorems for Complex Dynamics.
Springer, Heidelberg, 2010. 426 pages. ISBN 978-3-642-14508-7.
[bib | ⧉ | doi | book | web | errata | abstract]
-
André Platzer and Jan-David Quesel.
European Train Control System: A Case Study in Formal Verification.
Reports of SFB/TR 14 AVACS 54, 2009. ISSN: 1860-9821, www.avacs.org.
[bib | ⧉ | pdf | ICFEM'09]
-
André Platzer.
Differential Dynamic Logics:
Automated Theorem Proving for Hybrid Systems.
PhD Thesis, Department of Computing Science, University of Oldenburg, 2008.
ACM Doctoral Dissertation Honorable Mention Award in 2009.
Extended version appeared as book Logical Analysis of Hybrid Systems: Proving Theorems for Complex Dynamics, Springer, 2010.
[bib | ⧉ | pdf | eprint | slides | book | ebook | abstract]
-
André Platzer and Jan-David Quesel.
Logical verification and systematic parametric analysis in train control.
In Magnus Egerstedt and Bud Mishra, editors, Hybrid Systems: Computation and Control, 11th International Conference, HSCC 2008, St. Louis, USA, Proceedings, volume 4981 of LNCS, pp. 646-649. Springer, 2008. © Springer
[bib | ⧉ | pdf | doi | poster | abstract]
-
André Platzer.
Differential-algebraic dynamic logic for differential-algebraic programs.
Journal of Logic and Computation 20(1), pp. 309-352, 2010.
Special issue for selected papers from TABLEAUX'07. © The author
[bib | ⧉ | pdf | doi | eprint | study | errata | TABLEAUX'07 | abstract]
-
André Platzer.
Differential dynamic logic for hybrid systems.
Journal of Automated Reasoning 41(2), pp. 143-189, 2008. © The author
[bib | ⧉ | pdf | doi | mypdf | study | abstract]
-
André Platzer.
Differential dynamic logic for verifying parametric hybrid systems.
In Nicola Olivetti, editor, Automated Reasoning with Analytic Tableaux and Related Methods, International Conference, TABLEAUX 2007, Aix en Provence, France, July 3-6, 2007, Proceedings, volume 4548 of LNCS, pp. 216-232. Springer, 2007. © Springer
TABLEAUX Best Paper Award.
[bib | ⧉ | pdf | doi | slides | study | TR | abstract]
